Trigonometric identities

Trigonometric identities are essential tools for simplifying expressions and solving equations in mathematics. They are used in a wide range of disciplines, including architecture and engineering, physics, computer graphics, astronomy and medical imaging. Use this resource to learn about some of the fundamental identities, double angle formulas, sums and difference, and other trigonometric functions.

Trigonometric identities are equations involving trigonometric functions that are true for all values of the involved variables. For example, an expression such as:

\[\tan (\theta) =\frac{\sin (\theta)}{\cos (\theta)}\]

is true for ALL values of \(\theta\). So, we call this an identity.

To see how this is derived, remember that in any right-angled triangle:
\[\sin(\theta)=\frac{\textrm{Opposite}}{\textrm{Hypotenuse}}\] \[\cos(\theta)=\frac{\textrm{Adjacent}}{\textrm{Hypotenuse}}\] \[\tan(\theta)=\frac{\textrm{Opposite}}{\textrm{Adjacent}}\]

Therefore:
\[\frac{\sin(\theta)}{\cos(\theta)}=\frac{\frac{\textrm{Opposite}}{\textrm{Hypotenuse}}}{\frac{\textrm{Adjacent}}{\textrm{Hypotenuse}}}=\frac{\textrm{Opposite}}{\textrm{Adjacent}}=\tan(\theta)\]

Fundamental trigonometric identities

The expression \(\tan(\theta)=\dfrac{\sin(\theta)}{\cos(\theta)}\) is called a fundamental trigonometric identity. There are others, including one that is derived from the unit circle.

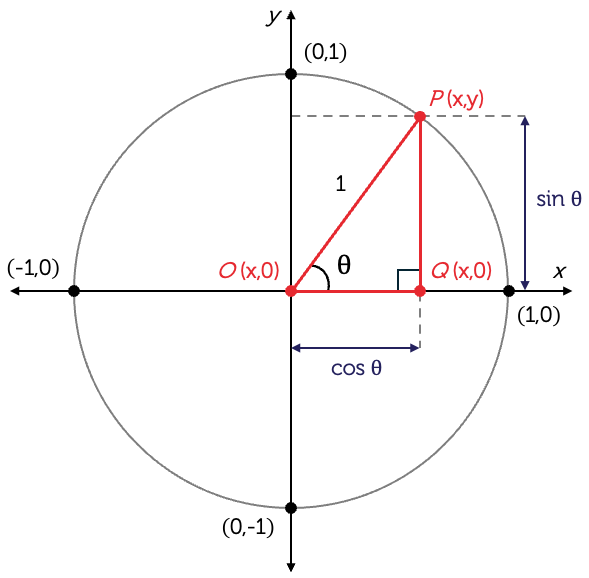
When we apply Pythagoras’ theorem to the right-angled triangle within the
unit circle, we find that \(\left(\sin\theta\right)^{2}+\left(\cos\theta\right)^{2}=1^{2}\), that is:

\[\sin^{2}(\theta)+\cos^{2}(\theta)=1\]

This is true for any value of \(\theta\).

Besides these two fundamental identities, there are many other trigonometric identities
that can be useful to simplify or rearrange trigonometric expressions.

Double angle formulas

As the name suggests, the double angle formulas are helpful when you deal with single angles \(\theta\) that have been doubled to \(2\theta\).

The sine double angle formula is:

\[\sin(2\theta) = 2\sin(\theta)\cos(\theta)\]

The cosine double angle formula is:

\[\begin{align*} cos(2\theta) & = \cos^{2}(\theta)-\sin^{2}(\theta)\\
& = 1-2\sin^{2}(\theta)\\
& = 2\cos^{2}(\theta)-1
\end{align*}\]

The tangent double angle formula is:

\[\tan(2\theta) = \frac{2\tan(\theta)}{1-\tan^{2}(\theta)}\]

Sums and differences formulas

The sums and differences formulas allow you to express trigonometric functions of sums or differences of angles in terms of the functions of the individual angles.

The sine sums and differences formulas are:

\[\begin{align*} \sin(x+y) & = \sin (x)\cos (y)+\cos (x)\sin (y)\\
\sin(x-y) & = \sin (x)\cos (y)-\cos (x)\sin(y)
\end{align*}\]

The cosine sums and differences formulas are:

\[\begin{align*} \cos(x+y) & = \cos (x)\cos (y)-\sin (x)\sin (y)\\
\cos(x-y) & = \cos (x)\cos (y)+\sin (x)\sin (y)
\end{align*}\]

The tangent sums and differences formulas are:

\[\begin{align*} \tan(x+y) & = \frac{\tan (x)+\tan (y)}{1-\tan (x)\tan (y)}\\
\tan(x-y) & = \frac{\tan (x)-\tan (y)}{1+\tan (x)\tan (y)}
\end{align*}\]

Reciprocal formulas

The reciprocal formulas are used for inverse trigonometric functions.

The reciprocal of cosine is cosecant, denoted by cosec or \(\csc\). It is given by:

\[\csc(\theta) = \frac{1}{\sin(\theta)}\]

The reciprocal of sine is secant, denoted by \(\sec\). It is given by:

\[\sec(\theta) = \frac{1}{\cos(\theta)}\]

The reciprocal of tangent is cotangent, denoted by \(\cot\). It is given by:

\[\cot(\theta) = \frac{1}{\tan(\theta)}=\frac{\cos(\theta)}{\sin(\theta)}\]

Example 1 – using trigonometric identities

Simplify \(\tan(x)\cos(x)\).

We can use the fundamental trigonometric identity: \(\tan(\theta)=\dfrac{\sin(\theta)}{\cos(\theta)}\).
\[\begin{align*} \tan (x)\cos (x) & = \frac{\sin (x)}{\cos (x)}\times\cos (x)\\
& = \sin (x)
\end{align*}\]

Exercise – using trigonometric identities

1. Show that \((\sec(x))(\cot(x))=\csc(x)\).
2. Simplify:
   1. \(\dfrac{\sin(2\theta)}{\sin(\theta)}\)
   2. \(\cos(2\theta)+2\sin^{2}(\theta)\)
3. Solve \(\sin^{2}(x)-\cos(x)-1=0\) for \(0\leq x\leq2\pi\).
4. Given that \(\sin\left(\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2}\), \(\sin\left(\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\), \(\cos\left(\dfrac{\pi}{3}\right)=\dfrac{1}{2}\) and \(\cos\left(\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\), find the exact value of \(\sin\left(\dfrac{\pi}{12}\right)\).